문제
반지름이 1, 2, ..., N인 원판이 크기가 작아지는 순으로 바닥에 놓여있고, 원판의 중심은 모두 같다. 원판의 반지름이 i이면, 그 원판을 i번째 원판이라고 한다. 각각의 원판에는 M개의 정수가 적혀있고, i번째 원판에 적힌 j번째 수의 위치는 (i, j)로 표현한다. 수의 위치는 다음을 만족한다.
- (i, 1)은 (i, 2), (i, M)과 인접하다.
- (i, M)은 (i, M-1), (i, 1)과 인접하다.
- (i, j)는 (i, j-1), (i, j+1)과 인접하다. (2 ≤ j ≤ M-1)
- (1, j)는 (2, j)와 인접하다.
- (N, j)는 (N-1, j)와 인접하다.
- (i, j)는 (i-1, j), (i+1, j)와 인접하다. (2 ≤ i ≤ N-1)
아래 그림은 N = 3, M = 4인 경우이다.
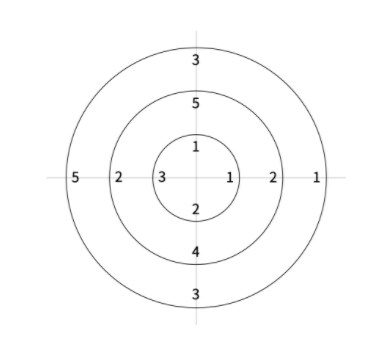
원판의 회전은 독립적으로 이루어진다. 2번 원판을 회전했을 때, 나머지 원판은 회전하지 않는다. 원판을 회전시킬 때는 수의 위치를 기준으로 하며, 회전시킨 후의 수의 위치는 회전시키기 전과 일치해야 한다.
다음 그림은 원판을 회전시킨 예시이다.
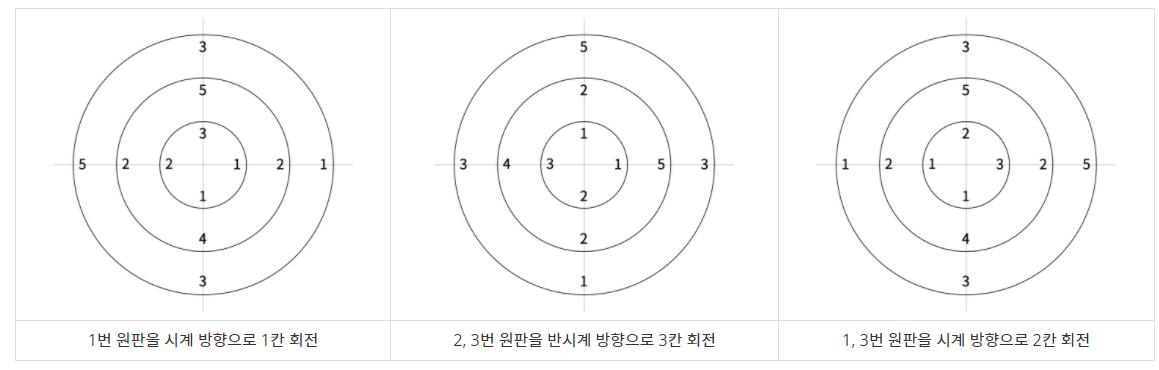
원판을 아래와 같은 방법으로 총 T번 회전시키려고 한다. 원판의 회전 방법은 미리 정해져 있고, i번째 회전할때 사용하는 변수는 xi, di, ki이다.
- 번호가 xi의 배수인 원판을 di방향으로 ki칸 회전시킨다. di가 0인 경우는 시계 방향, 1인 경우는 반시계 방향이다.
- 원판에 수가 남아 있으면, 인접하면서 수가 같은 것을 모두 찾는다.
- 그러한 수가 있는 경우에는 원판에서 인접하면서 같은 수를 모두 지운다.
- 없는 경우에는 원판에 적힌 수의 평균을 구하고, 평균보다 큰 수에서 1을 빼고, 작은 수에는 1을 더한다.
원판을 T번 회전시킨 후 원판에 적힌 수의 합을 구해보자.
입력
첫째 줄에 N, M, T이 주어진다.
둘째 줄부터 N개의 줄에 원판에 적힌 수가 주어진다. i번째 줄의 j번째 수는 (i, j)에 적힌 수를 의미한다.
다음 T개의 줄에 xi, di, ki가 주어진다.
출력
원판을 T번 회전시킨 후 원판에 적힌 수의 합을 출력한다.
제한
- 2 ≤ N, M ≤ 50
- 1 ≤ T ≤ 50
- 1 ≤ 원판에 적힌 수 ≤ 1,000
- 2 ≤ xi ≤ N
- 0 ≤ di ≤ 1
- 1 ≤ ki < M
구현해야할 조건
번호가 x의 배수인 원판은 d방향(0 : 시계, 1 : 반시계) k칸 회전시킨다. 원판에 수가 남아있으면, 인접하면서 수가 같은 것을 모두 찾으며, 그러한 수가 있으면 인접한 수를 지우고, 없는 경우에는 원판에 적힌 수의 평균을 구하고 평균보다 큰 수에서 1을 빼고, 작은 수는 1을 더한다. 평균 구하는 것을 잘 구해줘야 한다. (double)이용하는 것 생각해야 한다!
그리고 x의 배수 예를 들어 2라면 4,6,8,10 이렇게 진행이 되어야 하는데 초반에 2,4,8,16식으로 문제를 풀어서 시간을 손해 많이봤다. 천천히 읽고 분석하는 습관을 들이자! 그리고 인접한 숫자를 구하는데, 조건을 잘 파악하고 단순히 4방향에 인접한 애들이 있는지 찾으면 된다!
code
#include<iostream>
#include<queue>
#include<cstring>
#include<algorithm>
#define MAX 51
using namespace std;
const int dx[4] = {0,0,1,-1};
const int dy[4] = {1,-1,0,0}; // down, up, right, left
int n,m,T;
bool visited[MAX][MAX];
deque<int> dq[MAX];
int main()
{
cin >> n >> m >> T;
for(int i = 1; i <= n; i++)
{
for(int j = 0; j < m; j++)
{
int num;
cin >> num;
dq[i].push_back(num);
}
}
for(int tc = 0; tc < T; tc++)
{
int x,d,k; // x번째가 d 방향으로 k번 회전
cin >> x >> d >> k;
for(int i = 1; i <= n; i++) // x의 배수 문제를 잘못 파악했다!
{
if(i % x == 0)
{
if(d == 0) // 시계
{
for(int c = 0; c < k; c++)
{
int n = dq[i].back();
dq[i].pop_back();
dq[i].push_front(n);
}
}
else // 반시계
{
for(int c = 0; c < k; c++)
{
int n = dq[i].front();
dq[i].pop_front();
dq[i].push_back(n);
}
}
}
}
//인접한 숫자 바꾸기
memset(visited,false,sizeof(visited));
bool adjacent = false;
for(int i = 1; i <= n; i++)
{
for(int j = 0; j < m; j++)
{
if(dq[i][j] != 0) // 0이 아닌 애들로 구성
{
int y = i;
int x = j;
for(int i = 0; i < 4; i++) // 4방향 인접한 숫자가 있는지 확인하기!
{
int nx = x + dx[i];
int ny = y + dy[i];
if(0 <= nx && nx < m && 1 <= ny && ny <= n)
{
if(dq[ny][nx] != 0 && dq[ny][nx] == dq[y][x])
{
adjacent = true;
visited[ny][nx] = true;
}
}
}
if(x == 0)
{
if(dq[y][m-1] == dq[y][0])
{
adjacent = true;
visited[y][m-1] = true;
}
}
else if(x == m-1)
{
if(dq[y][0] == dq[y][m-1])
{
adjacent = true;
visited[y][0] = true;
}
}
}
}
}
if(!adjacent) // 인접한게 하나도 없다
{
int sum = 0;
int cnt = 0;
for(int i = 1; i <= n; i++)
{
for(int j = 0; j < m; j++)
{
sum += dq[i][j];
if(dq[i][j])
cnt++;
}
}
double avg = (double)sum / (double)cnt;
for(int i = 1; i <= n; i++)
{
for(int j = 0; j < m; j++)
{
if(!dq[i][j])
continue;
if(dq[i][j] > avg)
{
dq[i][j] -= 1;
}
else if(dq[i][j] < avg)
{
dq[i][j] += 1;
}
}
}
}
else // 인접한게 하나라도 있다.
{
for(int i = 1; i <= n; i++)
{
for(int j = 0; j < m; j++)
{
if(visited[i][j])
{
dq[i][j] = 0;
}
}
}
}
}
int res = 0;
for(int i = 1; i <= n; i++)
{
for(int j = 0; j < m; j++)
{
res += dq[i][j];
}
}
cout << res;
return 0;
}
'PS > Samsung' 카테고리의 다른 글
| [백준/c++] 19236 청소년 상어 (0) | 2022.02.17 |
|---|---|
| [백준/c++] 17825 주사위 윷놀이 (0) | 2022.02.15 |
| [백준/c++] 17837 새로운 게임 2 (0) | 2022.02.14 |
| [백준/c++] 17779 게리멘더링 2(다시풀어야돼) (0) | 2022.02.14 |
| [백준/c++] 17142 연구소 3 (0) | 2022.02.13 |



